Noise in quantum rigid rotors

Shubham Jain NIST-University of Maryland

Shubham Jain (a), Eric R. Hudson (b), Wesley C. Campbell (b), Victor V. Albert (a)

(a) Joint Center for Quantum Information and Computer Science, NIST and University of Maryland, College Park, MD, USA

(b) UCLA Center for Quantum Science and Engineering & Department of Physics and Astronomy, Los Angeles, California 90095, USA

Molecular rotational state spaces, modeled by infinite dimensional Hilbert spaces of quantum rigid rotors, present new grounds for robust quantum information processing. They are, however, prone to noise induced by the environment that surrounds them. As a step towards making qubits realizable through these rotor space configurations, we study and contrast the nature of two different types of noise that molecules would be prone to. The first is a generalization of the brownian center of mass motion for quantum rigid bodies in a thermal environment[1]. This kind of noise is found to be local in the angular position and angular momentum phase space of the rotor and hence, compatible with already existing molecular codes[2]. The second noise models blackbody radiation affecting the molecules[3],[4]. We show that this kind of noise can be highly non-local in the molecule’s phase space and characterize instances where conventional (i.e., exact) error-correction can fail. We comment on the different strategies that can circumvent this no-go result.

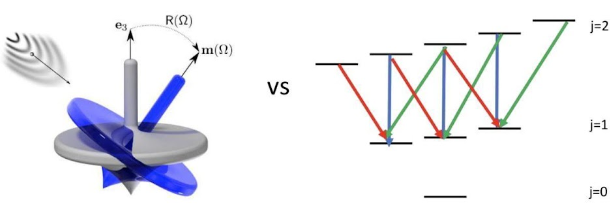
Figure 1. Visualization of the two types of noise - Quantum brownian motion[1] and Black body radiation in the presence of an environment

[1] B. A. Stickler, B. Schrinski, and K. Hornberger, Rotational Friction and Diffusion of Quantum Rotors, Phys. Rev. Lett. 121, 040401 (2018).

[2] V. V. Albert, J. P. Covey, and J. Preskill, Robust Encoding of a Qubit in a Molecule, Phys. Rev. X 10, 031050 (2020).

[3] Chessa, S., Giovannetti, V. Quantum capacity analysis of multi-level amplitude damping channels, Commun Phys 4, 22 (2021)

[4] Chessa, S. and Giovannetti, V., “Resonant Multilevel Amplitude Damping Channels”, arXiv:2207.05646v1(2022)

[4] Chen et al. arXiv:2210.13324